Task Interpreter Puzzle

in Notes on Reversing, Puzzle
Task Interpreter Puzzle

The solution often turns out more beautiful than the puzzle. - Richard Dawkins

Intro

It was around lunch hour when I received a ping from a good friend and colleague of mine. He sent me a task_interpreter.py file and asked me if I could solve the challenge. I managed to have a look at it but it seemed a bit tough honestly, wrote some comments on the file and decided to shelf it to my long to-do list.

On Friday while at work, my colleague (he is also a good friend of mine 😂) asked me if I had taken a look at the challenge. We sat down with him and I explained to him what I had understood about the challenge and in the process, I got a better understanding of the challenge. That evening I decided to have a look at the challenge and two days later I was able to solve the challenge and call it a success.

This post will describe my thought process when solving the challenge and what I would conclude as the teaching lesson.

The Code

# file: "task_interpreter.py"
import struct
from hashlib import sha256
from binascii import hexlify, unhexlify
from Crypto.PublicKey import RSA


STACK_MAX_SIZE = 128
PROGRAM_MAX_SIZE = 2048

STACK = []

def op_nop(code):
	return 0

def op_push(code):
	off = 0
	if len(code) < 1:
		raise Exception("Opcode processing error")

	l = struct.unpack('B', code[off:off+1])[0]
	off += 1

	if len(code[off:]) < l:
		raise Exception("Opcode processing error")

	STACK.append(code[off:off+l])
	off += l

	return off

def op_dup(code):
	if len(STACK) < 1:
		raise Exception("Opcode processing error")

	STACK.append(STACK[-1])
	return 0

def op_equal(code):
	if len(STACK) < 2:
		raise Exception("Opcode processing error")

	STACK.append(bytes([STACK.pop() == STACK.pop()]))
	return 0

def op_hash(code):
	if len(STACK) < 1:
		raise Exception("Opcode processing error")

	STACK.append(sha256(STACK.pop()).digest())
	return 0

def op_verify(code):
	if len(STACK) < 1:
		raise Exception("Opcode processing error")

	if STACK.pop() == b'\x00':
		raise Exception("Verify failed")
	return 0

def op_check_sig(code):
	if len(STACK) < 3:
		raise Exception("Opcode processing error")
	
	pub_key = STACK.pop()
	msg = sha256(STACK.pop()).digest()
	sig = STACK.pop()

	msg = int.from_bytes(msg, 'big')
	if len(pub_key) < 129:
		raise Exception("Opcode processing error")
	n = int.from_bytes(pub_key[:128], 'big')
	e = int.from_bytes(pub_key[128:], 'big')
	sig = int.from_bytes(sig, 'big')

	pub_key = RSA.RsaKey(n=n, e=e)
	STACK.append(bytes([pow(sig, pub_key.e, pub_key.n) == msg]))
	return 0

OPS = {
	0: op_nop,
	1: op_push,
	#2: op_add,
	#3: op_sub,
	#4: op_not,
	6: op_dup,
	7: op_equal,
	8: op_hash,
	9: op_verify,
	0x0c: op_check_sig,
	# 0x0d: op_halt
}

def process(code):
	pc = 0
	while pc < len(code):
		f = OPS.get(code[pc], None)
		if not f:
			raise Exception(f'Wrong opcode {code[pc]}')

		pc += f(code[pc+1:]) + 1

		if len(STACK) > STACK_MAX_SIZE:
			raise Exception("Stack size exceeds")

def solve(lock, unlock):
	if len(lock) > PROGRAM_MAX_SIZE or len(unlock) > PROGRAM_MAX_SIZE:
		return False

	process(unlock)
	process(lock)

	if STACK[0] == b'\x01':
		return True

	return False

lock = b''
lock += b'\x08'
lock += b'\x01\x20\x9f\x86\xd0\x81\x88\x4c\x7d\x65\x9a\x2f\xea\xa0\xc5\x5a\xd0\x15\xa3\xbf\x4f\x1b\x2b\x0b\x82\x2c\xd1\x5d\x6c\x15\xb0\xf0\x0a\x08'
lock += b'\x07'
lock += b'\x09'
lock += b'\x01\x83\xb8\x1d\x31\x39\x5e\xd5\xf6\xb7\x14\xac\x1e\x12\xaa\x4a\x72\xca\x24\x7f\xce\x87\x8a\xe6\xf9\x04\x25\xb1\x82\x35\xff\x99\xb1\xf0\x9f\x98\xd3\xfb\xdb\x6d\xeb\x0b\x35\x6f\x63\x51\x67\x44\x8c\x66\x66\xb9\x5c\x44\xb5\x3a\x81\x5b\xce\xbf\xeb\xb2\x2a\x34\x71\xd1\x94\x85\xad\xca\x7f\x30\x37\x7d\xb5\x56\x46\x78\x4c\xe8\xa7\x6f\x43\xcf\x0a\x2d\x32\x13\x76\x5d\x10\xe1\x9f\xe3\xc5\x19\x74\xe9\x69\xe1\xfa\x5b\x71\x4c\x9d\x9c\x0c\x35\xcf\xe8\x53\x2d\x12\xa6\x23\x1e\xd4\x9c\x59\xd3\xab\x81\xa2\x36\x50\x18\x55\xdf\x35\xd1\x01\x00\x01'
lock += b'\x0c'

unlock = unhexlify(input('Enter the script to solve the puzzle: '))
if solve(lock, unlock):
	print('Great job!')
else:
	print('Try again :(')

The code contains nine functions; op_nop, op_push, op_dup, op_equal, op_hash, op_verify, op_check_sig, process and solve. It also contains one list, one dictionary, and four variables; STACK, OPS, STACK_MAX_SIZE, PROGRAM_MAX_SIZE, lock, and unlock respectively.

At a glance when looking at the first nine instructions they work like VM instructions. The process function works as described and the solve function checks if we have solved the puzzle.

The OPS dictionary contains keys that act as the op_codes and the values which are our instructions functions. Our lock variables already contain data that we will later analyze.

The PROGRAM_MAX_SIZE is equal to 2048 and the STACK_MAX_SIZE is equal to 128.

The Puzzle

The program requires us to input some data in hex which is going to be converted back from hex to binary data (bytes). Our input is then stored in a variable called unlock which is then passed to the solve function in an if statement. If the return value from our solve function is true, it prints Great job! and if it’s false it prints Try again :(.

The solve function takes two variables lock and unlock. It first checks the length of both variables and if any of them are greater than the PROGRAM_MAX_SIZE it will return a false. If the lengths are within bounds it calls the process function twice when passing the unlock and lock variables respectively. Then proceeds to check if the first element in our STACK is equal to byte \x01 it returns true and if it’s not equal it returns false.

The process function takes in one variable code. First initializes program counter pc to zero which is the length of our byte code. Then proceeds to a while loop that checks if the pc is less than the length of our code. Inside the while loop, it initializes the function f which checks the first byte in our code and maps it with the key value in our OPS dictionary. If the key value isn’t present it raises an error printing Wrong opcode [value]. The next line of code is the one that prevents the while loop from being an infinite loop. Once the key value has been found and data has been passed to our specified instruction function, the specified instruction returns a value either the length of the code or zero which is then incremented by one so that pc to be greater than the length of code. Afterward, it checks if the data in the STACK is greater than the STACK_MAX_SIZE and if it is it raised an error printing Stack size exceeds.

Instruction functions

Each instruction function performs a task using either the input data code or the data in the STACK. I won’t explain the finer details of each line in the function but only the important bits and pieces.

  • op_push; adds data to the STACK and returns the length of the input data.
  • op_dup; duplicates the last element in the STACK and returns zero.
  • op_equal; pops the last two elements in the STACK and checks if they are equal. Where it appends byte \x01 or \x00 to the STACK if they are equal or not equal respectively. It also returns zero.
  • op_hash; pops the last element in the STACK and appended its sha256 digest (hash value) to the STACK. It also returns zero.
  • op_verify; pops the last element in the STACK and checks if it is equal to byte \x00 it raises an error printing Verify failed. It also returns zero.
  • op_check_sig; pops the last three elements in the stack and points them to variables pub_key, msg, and sig respectively. Then proceeds to prepare the data to perform an RSA verify signature algorithm.

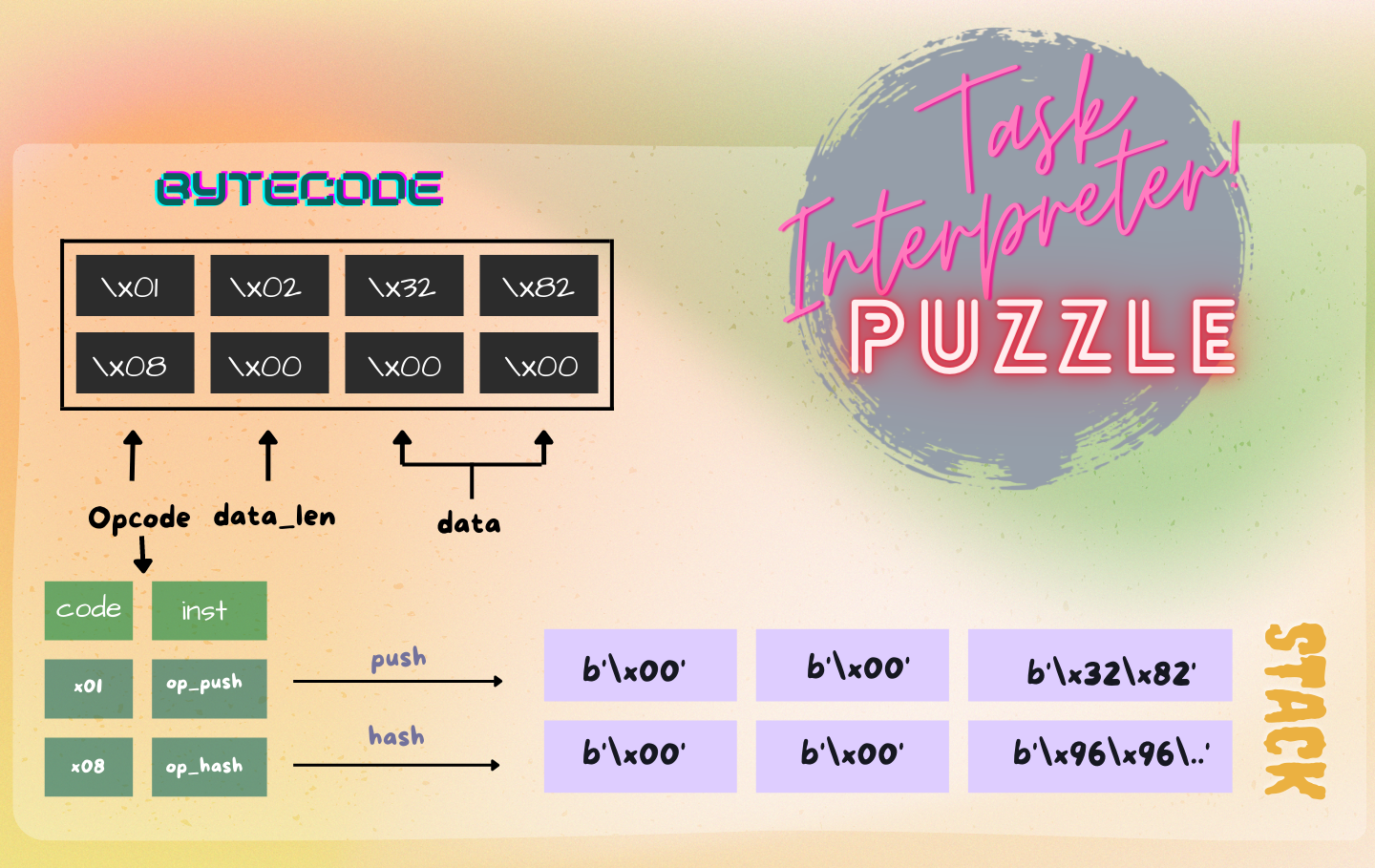
Bytecode data

I figured out the bytecode data format by looking at the lock data. This will be important for solving the challenge because we need to understand how the process takes in data to solve the challenge. The first byte data is the op_code and the second-byte data is the data_len length of the data following it. The length is mainly required when pushing the data to the stack.

image2

bytecode data format

Thought process

I noticed that our input data is being processed first then the lock data. That being the case I worked with what I had the lock data.

lock = b''
lock += b'\x08'
lock += b'\x01\x20\x9f\x86\xd0\x81\x88\x4c\x7d\x65\x9a\x2f\xea\xa0\xc5\x5a\xd0\x15\xa3\xbf\x4f\x1b\x2b\x0b\x82\x2c\xd1\x5d\x6c\x15\xb0\xf0\x0a\x08' # msg_hash
lock += b'\x07'
lock += b'\x09'
lock += b'\x01\x83\xb8\x1d\x31\x39\x5e\xd5\xf6\xb7\x14\xac\x1e\x12\xaa\x4a\x72\xca\x24\x7f\xce\x87\x8a\xe6\xf9\x04\x25\xb1\x82\x35\xff\x99\xb1\xf0\x9f\x98\xd3\xfb\xdb\x6d\xeb\x0b\x35\x6f\x63\x51\x67\x44\x8c\x66\x66\xb9\x5c\x44\xb5\x3a\x81\x5b\xce\xbf\xeb\xb2\x2a\x34\x71\xd1\x94\x85\xad\xca\x7f\x30\x37\x7d\xb5\x56\x46\x78\x4c\xe8\xa7\x6f\x43\xcf\x0a\x2d\x32\x13\x76\x5d\x10\xe1\x9f\xe3\xc5\x19\x74\xe9\x69\xe1\xfa\x5b\x71\x4c\x9d\x9c\x0c\x35\xcf\xe8\x53\x2d\x12\xa6\x23\x1e\xd4\x9c\x59\xd3\xab\x81\xa2\x36\x50\x18\x55\xdf\x35\xd1\x01\x00\x01' #pub_key
lock += b'\x0c'
  1. Starts by calling the op_hash instruction which will hash the last element in the STACK.
  2. Pushes some data of length 32 to the STACK.
  3. Calls the op_equal instruction which will compare the last two elements in the STACK.
  4. Calls the op_verify instruction which will verify if the last two elements were equal.
  5. Pushes some data of length 131 to the STACK.
  6. Then proceeds to call the op_check_sig instruction.

From the lock data I verified two things, one is that the first data being pushed to the STACK is a sha256 hash digest because the first instruction hashes some data that will be in the stack then later on checking if they are equal to each other and verifying that they were equal. Two is that the last data being pushed before calling op_check_sig is a pub_key. When the op_check_sig is called you could see that the last element is set to the pub_key variable.

I will be honest at first I thought this was a hash collision attack kind of challenge but after reviewing the op_check_sig instruction noticed that it wasn’t. Because I have never done any cryptography kind of challenge I went ahead and checked for CTF writeups that involved RSA to learn about it and read also about RSA in the book Serious Cryptography by Jean-Phillipe Aumasson.

Learned a few things when trying to figure out if that instruction was vulnerable and ended up having a quick chat with a friend on discord who was able to crack the msg_hash using the crack station site. My friend also informed me that the op_check_sig instruction was not vulnerable to textbook RSA signature attacks because n was not vulnerable.

image3

I don’t understand how I forgot to try and crack the hash.

I thought I had hit a dead-end because for us to solve this puzzle we are required to have a byte \x01 at the beginning of the stack which I thought we would have got by passing the verify signature algorithm being performed by op_check_sig instruction.

Solving

As I was heading to work on Tuesday I got a light bulb moment, we have control of what we place in the STACK what if we could find a way to place the byte \x01 at the beginning of the stack and despite whatever is appended after the last instruction we will still have our byte present.

To attain this I first noted what data will be popped from the STACK by each instruction so that the byte should be present at the end. Because now we have the msg it means we can pass the verification being performed in steps 3 and 4.

# file: "solve.py"
#!/usr/bin/env python3
"""
Solve task interpreter puzzle challenge
"""

import struct
from hashlib import sha256
from binascii import hexlify, unhexlify

STACK_MAX_SIZE = 128
PROGRAM_MAX_SIZE = 2048

STACK = []

def op_push(code):
    off = 0
    if len(code) < 1:
        raise Exception("Opcode processing error")

    # finds length of unpacked code...
    l = struct.unpack('B', code[off:off+1])[0]

    off += 1
    
    if len(code[off:]) < l:
        raise Exception("Opcode processing error")

    STACK.append(code[off:off+l])
    off += l

    return off

def op_dup(code):
    if len(STACK) < 1:
        raise Exception("Opcode processing error")

    STACK.append(STACK[-1])
    return 0

def op_equal(code):
    if len(STACK) < 2:
        raise Exception("Opcode processing error")

    STACK.append(bytes([STACK.pop() == STACK.pop()]))
    return 0

def op_hash(code):
    if len(STACK) < 1:
        raise Exception("Opcode processing error")

    STACK.append(sha256(STACK.pop()).digest())
    return 0

def op_verify(code):
    if len(STACK) < 1:
        raise Exception("Opcode processing error")

    if STACK.pop() == b'\x00':
        raise Exception("Verify failed")
    return 0

OPS = {
    1: op_push,
    6: op_dup,
    7: op_equal,
    8: op_hash,
    9: op_verify,
}

def process(code):
    pc = 0
    while pc < len(code):
        f = OPS.get(code[pc], None)
        
        if not f:
            raise Exception(f'Wrong opcode {code[pc]}')

        pc += f(code[pc+1:]) + 1

        if len(STACK) > STACK_MAX_SIZE:
            raise Exception("Stack size exceeds")

msg = b'\x01\x04\x74\x65\x73\x74'
sig = b'\x01\x01\x00'

unlock = b''
unlock += msg
unlock += b'\x06'
unlock += b'\x07'
unlock += sig
unlock += msg
unlock += b'\x06'

print(hexlify(unlock))

process(unlock)

print(STACK)

Most of the logic in my script is borrowed from the puzzle. I first specified two variables msg and sig where the message is the value cracked from our msg_hash and signature is a null byte \x00.

Remember when the op_sig instruction is called it will pop three values from the stack. These two variables were our missing pieces.

My unlock data do the following;

  1. Push message test to the STACK.
  2. Call op_dup instruction which will duplicate our message.
  3. Call op_equal instruction which will manage to produce the byte \x01 and place it as the first element in our STACK.
  4. Push signature to the stack which will be popped by the op_check_sig instruction.
  5. Push message to the STACK.
  6. Call op_dup instruction which will duplicate our message where the last message will be hashed by lock data for it to pass the verification.

image4

Conclusion

This was an interesting puzzle to solve. This was an interview question and I think the main idea was to test the interviewee on source code review.

If you find any other way of solving the challenge by passing the verify RSA signature algorithm please feel free to share would love to learn from you.

Resources

© GR00T